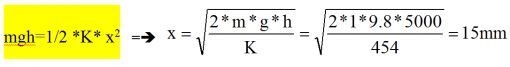PROBLEM 1
PROBLEM 1. : Yüksekten düşen bir cisim kirişi nasıl deforme eder Yanlış soru: 5 metre yüksekten düşen 1 Kg ağırlığında bir Doğru Soru: 5 metre yüksekten düşen 1 Kg ağırlığındaki bir |
 | |
Ülkemizde bir çok kişide hatta bazı mühendislerde yanlış bir kanı vardır. O yanlış kanı yüksekten düşen cismin çarptığı yere ağırlığının 5-10 katı kadar şok kuvvet uyguladığı şeklindedir. Önce şu yanlışı düzeltelim. Şok kuvvet diye bir şey yoktur. Şok enerjinin bir şekilden başka bir şekle çok hızlı geçmesi ile oluşan etkidir. Ancak sonucu itibariyle bir kütlenin çarptığı yerde yarattığı etkinin kendi kütlesinden kat be kat fazla bir kütlenin yaratacağı etkiye eşit olması nedeni ile bu etkiyi yapabilecek kütlenin ne olduğu çarpan kütlenin ŞOK FAKTÖRÜ ile çarpılması ile bulunur. (Bu etkiyi yaratan kuvvet değil hızlanmış kütlenin kazandığı enerjidir). Yukarıdaki soruya geri dönersek; Oluşacak deformasyon tamamen çarpan cismin ve çarptığı kirişin şekline ve malzeme özelliklerine bağlıdır. Eğer çarpan ve çarpılan malzemenin elastikiyet derecesi yeteri kadar yüksek ise deformasyon olmaz fakat malzeme esner. Eğer elastikiyet yeterli değilse çarpanda ve çarpılanda bir miktar deformasyon olur, bir miktar enerji de esneme yolu ile emilir. | ||
Şimdi yukarıdaki soruyu tamamlayarak tekrar soralım. 5 metre yüksekten düşen 1 Kg ağırlığındaki bir kütle çarpmış olduğu Cevap: Çarpan kütlenin hiç deforme olmayacak kadar sert olduğunu ve geriye sekmeyeceğini kabul edersek. 1. Düşen malzemenin çarptığı noktada aktardığı enerji (yapılan iş) W=mgh = 1 Kg * 9.8 m/sn² * 5000 mm = 49,000 N-mm 2. Kirişin elastikiyet kat sayısı “K” (yay sabiti) | 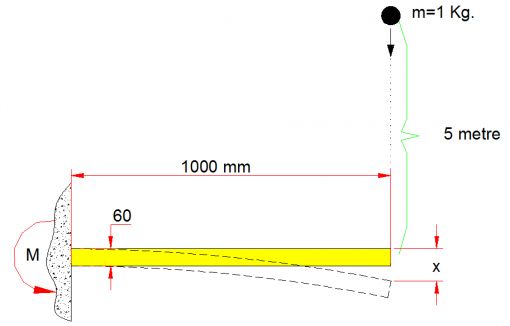 | |
 |
I : Kirişin atalet momenti (mm4) E= 210,000 N/mm² (Çelik için) L= 1,000 mm.
h= kiriş yüksekliği= 60 mm. b= kiriş genişliği =40 mm | |
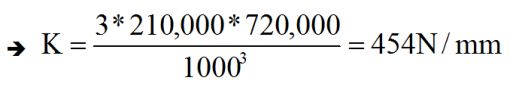 | ||
| Enerji denkleminde yerine koyarsak | ||
| ||
Böylece çarpan kütlenin ankastre kirişte 15 mm lik bir seğime sebeb olduğunu bulduk. Ancak bu seğim kalıcı bir deformasyonmu yoksa esnememi? Bunu anlamak için kirişte ortaya çıkan gerilimi hesap etmemiz gerekir. | ||
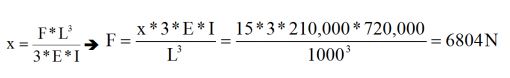 | ||
Kirişte oluşan maksimum moment: M=F*L= 6,804*1,000 = 6,804,000 N-mm Nominal eksen kirişin tam ortasından geçtiğinden  | 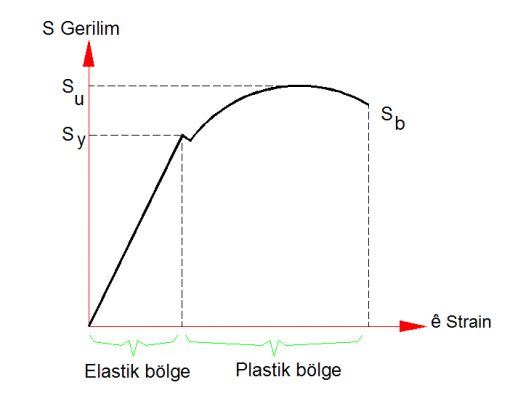 | |
Kiriş malzemesinin St37-2 olduğunu kabul edersek, bu malzemenin çekme dayanımını TABLO dan | ||
NOT: Bu cevaplarda çarpanda bir deformasyon olmayacağı kabul edilmiş olduğu gibi çarpmanın olduğu noktada da kirişin ezilmeyeceği ve çarpan cismin geri sekmeyeceği kabul edilmiştir. Normalde hem kiriş hemde çarpan cisimde ezilme olur ve çarpan da bir miktar geri seker. Bu nedenle enerjinin bir kısmı bu işlere harcanır, geri kalan ise kirişi büker. Yani kirişin deformasyon miktarı hesap edilenden daha az olur. | ||
| GERİ DÖN | ||